Imagine for a moment that you were a point in multidimensional space, and your nearby neighbors in this space are people that share your preferences for restaurants, bars, and clubs. In this model, a bar you like is very near to you (e.g., by a Euclidean metric), while some place you hate is far away.
This model rules Yelp. A review on yelp is a measurement of the distance between the reviewer and the reviewed. The review will be favorable if and only if the reviewer is nearby the reviewed in the model.
A restaurant (e.g., Bite) gets good reviews because the people that review it know or can guess, before they go there, that they will like it. If they didn't, the place wouldn't have such stellar reviews.
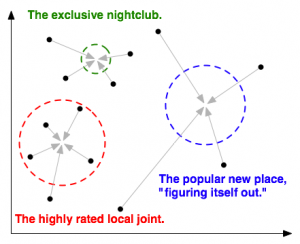
So why do some places get terrible reviews? I see cases that would cause this. First, if a new nightclub (e.g., Universal) is still "figuring itself out," it might attract a lot of people expecting one thing and getting another. In other words, they are not near the place in the model, but they visit it anyway because they think they might. Likely, because the place is so new, many people are testing it out, so you can expect the reviews to be unfavorable, even by the people who are supposed to like it, because the presence of outsiders ruins the whole experience.
In another case, a super-exclusive bar might only cater to a very narrow range of clientele. In other words, you have to be unusually close to this bar in the model in order to like it. Perhaps it only supports one or two cliques of regulars, and everyone else is shunned.
In this example, the radii correspond to the ability of a bar or restaurant to support a wide or narrow section of people.